信奥教你的第二件事：复杂问题可以拆成小问题

任何一个复杂问题，之所以显得复杂，往往是因为我们试图一次性解决它。

在信息学奥赛的训练过程中，每一位选手都会经历这样一个转折点：面对一道从未见过的难题，从最初的恐慌茫然，到冷静地将其拆解为若干个可处理的子问题，然后逐个击破。这个过程不仅是算法能力的提升，更是一种思维方式的蜕变。

一、分解思想：从生活到代码

分治策略的核心思想其实源于日常生活。正如学习中的目标分解——把期末考试的好成绩，拆分为语文、数学、英语各科的好成绩，再继续拆分为具体的知识点掌握。信息学奥赛中的问题分解，正是这种思维在编程中的体现。

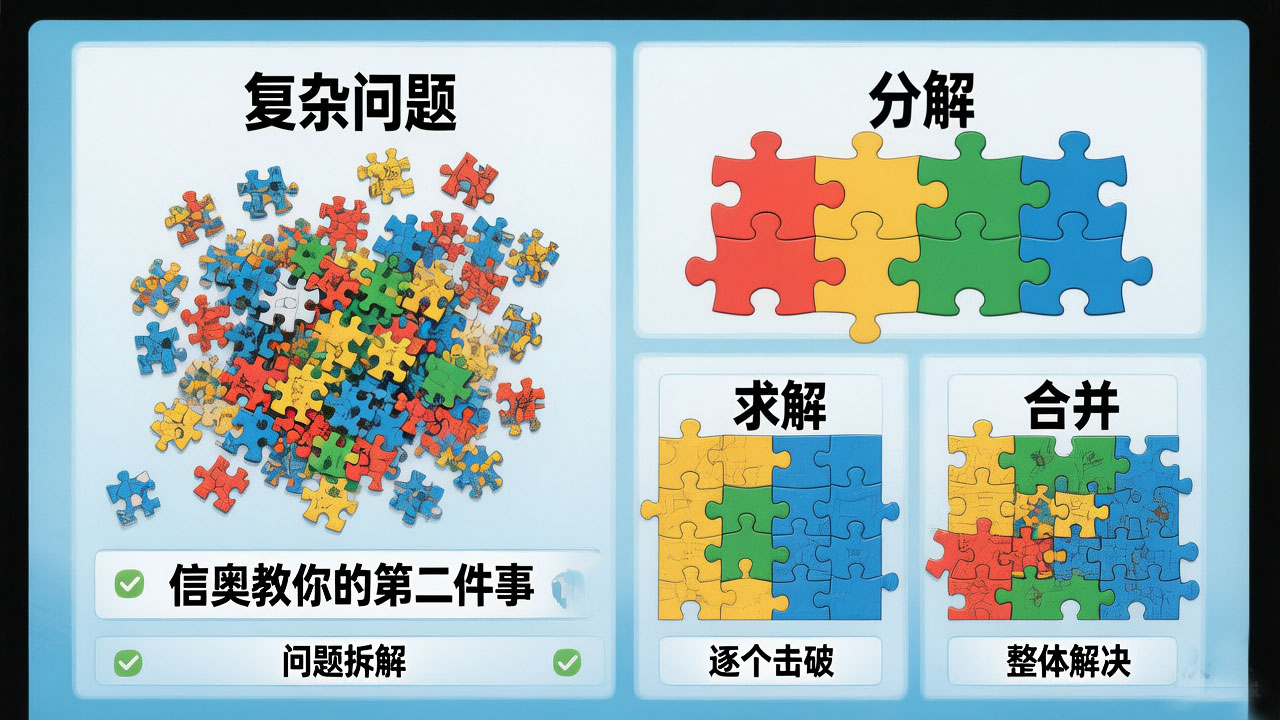
分治法解题的一般步骤包括三个环节：首先是分解，将要解决的问题划分成若干规模较小的同类问题；其次是求解，当子问题划分得足够小时，用较简单的方法解决；最后是合并，按原问题的要求，将子问题的解逐层合并构成原问题的解。

这种思想在信奥赛中的价值体现在两个层面：一是算法设计层面，如归并排序、快速排序等经典算法；二是解题策略层面，将一个复杂问题拆分为多个相对独立的模块分别实现。

二、经典分治：从排序到归并

以经典的归并排序为例，它完美展示了分治思想的三个步骤：

1. 分解：将待排序的n个元素分成两个规模为n/2的子序列

2. 求解：递归地对两个子序列进行归并排序

3. 合并：将两个已排序的子序列合并成一个完整的有序序列

这种方法的时间复杂度为O(n log n)，远优于简单排序算法的O(n²)。更重要的是，归并排序的思路可以推广到许多看似与排序无关的问题，如求解逆序对、计算最大子段和等。

另一个典型应用是快速排序，它通过选择一个基准元素，将原问题分解为两个相对独立的子问题——左侧小于基准的部分和右侧大于基准的部分，然后递归处理。这种"分而治之"的策略，使得复杂问题迎刃而解。

三、问题拆解的艺术：从三维偏序到CDQ分治

随着信奥竞赛难度的提升，问题拆解的艺术也愈发精深。CDQ分治是一种巧妙的分治思想应用，它专门用于解决多维偏序问题。

考虑这样一个问题：有N个选手，每人有三次竞赛的排名，要找出在所有竞赛中都比别人靠前的"优秀"选手。这是一个典型的三维偏序问题——需要同时比较三个维度的排名。

CDQ分治的解决思路体现了问题拆解的层次性：

• 第一维排序：先按第一次竞赛排名排序，保证第一维有序

• 第二维分治：将序列分成左右两半，左半边的第一维一定小于右半边

• 第三维统计：在分治过程中，将满足前两维要求的元素投射到第三维，用树状数组统计

这种层层递进的分解方式，将一个看似复杂的三维比较问题，转化为一系列有序的二维和一维子问题。

四、拆分与贪心：纪念品分组问题

纪念品分组问题是另一个体现分解思想的经典案例。问题描述如下：有若干件纪念品，每个有特定价格，需要将它们分组，每组最多两件且总价不能超过上限w，问最少需要多少组。

这个问题的解决思路可以通过以下步骤分解：

1. 排序预处理：将纪念品按价格升序排序

2. 双指针扫描：设左指针指向最小价格，右指针指向最大价格

3. 贪心决策：如果最便宜的与最贵的可以一组，则配对成功；否则最贵的单独一组

这种"排序+双指针"的解法，本质上是将复杂的组合优化问题拆解为一系列简单的二元决策。每一步只关注当前最"极端"的两个元素，通过局部最优选择达到全局最优。

五、根号分治：复杂度的平衡艺术

在信奥竞赛中，有一种独特的问题拆解方法叫根号分治。它不直接拆分问题本身，而是根据数据规模选择不同的算法策略。

例如在哈希冲突问题中，对于模数p较小和较大的情况，采用截然不同的处理方式：

• 当模数 p ≤ √n 时，通过预处理将结果存储起来，实现O(1)查询

• 当模数 p > √n 时，直接暴力计算，因为跳跃次数不会超过√n

这种方法的精髓在于认识到：没有一种算法能完美处理所有情况，但通过将问题按规模拆解，选择不同策略，可以平衡预处理与查询的复杂度，达到整体最优。这是一种更高层次的"问题拆解"——将问题的求解策略本身作为拆解的对象。

六、从竞赛到生活：思维方式的迁移

信息学奥赛中培养的"拆解复杂问题"的能力，其价值远超竞赛本身。分治法解题必须满足的几个条件，恰好对应着解决现实复杂问题的关键要素：

1. 问题可以分解：现实中的复杂项目，往往可以拆分为相对独立的子任务

2. 子问题同类：分解后的子任务与原问题在结构上相似，便于使用相同的方法论

3. 解可合并：各个子任务的解决方案最终能够整合为整体解决方案

在信奥复赛中，有经验的选手会采用"部分解题，积少成多"的策略。如果一个问题很难完全解决，就尝试解决它的一个子问题，获得部分分数。这种策略不仅适用于比赛，也适用于日常学习——将宏大的学习目标分解为每日可执行的小任务。

七、实例分析：糖果游戏中的分治思想

以信奥一本通中的糖果游戏问题为例，五个小朋友围坐一圈，各自有若干糖果，每个小朋友同时将自己糖果分成三份，给左右邻居各一份，自己留一份。

这个问题的直接模拟看似简单，但若按顺序处理会导致逻辑混乱。正确的分解方式是：将"同时分糖"拆解为"记录原状态→计算新值→更新状态"三个步骤，每个步骤单独处理，最后合并结果。

这种分解不仅使代码逻辑更清晰，也避免了因顺序处理而产生的错误。

结语：分而治之的智慧

信息学奥赛教会我们的第二件事，就是将复杂问题拆解为小问题的能力。无论是归并排序的分治策略，CDQ分治的层层递进，纪念品分组问题的贪心决策，还是根号分治的策略选择，都体现着同一个思想：复杂问题并不可怕，可怕的是试图一口吃成胖子。

对于信奥选手而言，掌握问题拆解的艺术，意味着在遇到任何难题时，都能冷静地问自己：这个问题可以分解为哪些子问题？这些子问题之间是什么关系？如何将子问题的解组合成原问题的解？

这种思维方式，不仅是编程竞赛的制胜法宝，更是解决现实世界复杂问题的通用智慧。正如一位信奥教练所言："分治法解题的关键，不在于你有多聪明，而在于你有多懂得把大问题变小，把小问题变没。"

下一次，当你面对一道看似无从下手的信奥题目时，请记住：复杂问题可以拆成小问题。这个道理，就是信奥要教给你的第二件事。